E-411 PRMA
Lecture 9 & 10 - Item Response Theory
Item analysis
Many different ways to analyze items
Can focus on
Difficulty of item
Reliability of item
Validity of item
Discrimination of item
Issues in Test Development
Guessing
Bias in favor of one group - differential item functioning
Test length and duration of testing session
Alternatives to item analysis
Think Alouds
Expert Panels
Interviews
Qualitative Methods
Test Revision
On what basis should we revise our items?
Too easy or too hard items?
Items with similar difficulty that are measuring the same concept?
Items with negative point-biserial correlations?
Items that on a second/third read through seem unrelated to the construct?
Items with low factor loadings?
Based on IRT?
Standardization
We settle on our revisions
Administer revised version to new sample
This becomes our comparsion group, our standardization sample
Revising old tests
Tests need to be revised when the domain has significantly changed
Content of the items is not understood or changed
Test norms are no longer adequate
Theory underlying the domain has changed
Reliability and validity of the instrument can be improved
Cross- and co-validation
Cross-validation - revalidation of a test on a seperate, independent sample of testtakers
Item validities should shrink during this process (validity shrinkage)
Co-validation - test validation conducted on two or more tests with the same sample of testtakers
Creating norms, co-norming
Cheaper, reduces sampling error by norming on the same sample
Today
Item Response Theory
Review
Classical Test Theory
X = T + E
\(\sigma^2_X = \sigma^2_T + \sigma^2_E\)
\(\sigma_{\text{SEM}} = \sigma \sqrt{1 - r_{xx}}\)
Critiques of CTT
- Person are measured on number correct
- Score dependent on number of items on a test and their difficulty
- Scores are limited to fixed values
- Scores are interpretable on a within-group normative basis
- SEM is group dependent and constant for a group
- Item and person fit evaluation difficult
- Test development different depending on type of test
Item Response Theory Rationale
In an nutshell, IRT is able to address all of these criticisms
BUT, makes stronger assumptions and requires a larger sample size
What is Item Response Theory?
A measurement perspective
A series of non-linear models
Links manifest variables with latent variables
Latent characteristics of individuals and items are predictors of observed responses
Not a "how" or "why" theory
Generalized Anxiety Disorder
Anxiety could be loosely defined as feelings that range from general uneasienss to incapcitating attacks of terror
Is anxiety latent and is it continuous, categorical, or both?
Categorical - Individuals can be placed into a high anxiety latent class and a low anxiety latent class
Continuous - Individuals fall along an anxiety continuum
Both - Given a latent class (e.g. the high anxiety latent class), within this class there is a continuum of even greater anxiety.
How to measure generalized anxiety?
- Used observed (i.e. manifest variables) that provide a proxy of generalized anxiety
- These provide our operationalized definition of generalized anxiety
- But how do we put these observed measures onto the generalized anxiety scale?
Properties of IRT
- Manifest variables differentiate among persons at different locations on the latent scale
- Items are characterized by location and ability to discriminate among persons
- Items and persons are on the same scale
- Parameters estimated in a sample are linearly transformable to estimates of those parameters from another sample
- Yields scores that are independent of number of items, item difficulty, and the individuals it is measured on, and are placed on a real-number scale
Assumptions of IRT

Response of a person to an item can be modeled with the a specific item reponse function
Item parameters
IRT: Item parameters estimated in one sample from a population are linearly transformable to estimates of those parameters on another sample from the same population. This makes it possible to create large pools of items that have been linked by this transformation process onto a common scale.
Unlike CTT, equating occurs automatically as a result of linking, without assumption of score distributions. This makes it possible to compare on a common scale persons measured in different groups and with different items.
Other traits of IRT
- Use test information function for designing a test
- Has methods for examing item fit for identifying items that misfit
- Has methods for examing person fit for identifying persons that misfit
- Adaptive testing can be implemented (e.g. CAT)
- IRT is a family of models for various response types and could be used with multidimensional data.
IRT conceptually
Item Response Function (IRF)

The Rasch Model
The logistic model
\(p(x = 1 | z) = \frac{e^z}{1 - e^z}\)
The logistic regression model
\(p(x = 1 | g) = \frac{e^{\beta_0 + \beta_1g}}{1 - e^{\beta_0 + \beta_1g}}\)
The Rasch model
\(p(x_j = 1 | \theta, b_j) = \frac{e^{\theta - b_j}}{1 - e^{\theta - b_j}}\)
So, the Rasch model is just the logistic regression model in disguise
What does \(\theta - b_j\) mean
rasch <- function(person, item) {
exp(person - item\) (1 + exp(person - item))
}
rasch(person = 1, item = 1.5)
# [1] 0.3775407
rasch(person = 1, item = 1)
# [1] 0.5
Getting item correct recap
For the 1-PL and the Rasch, the probability of getting an item correct is a function of the distance an item is located from a person.
For the 2-PL, this is also a function of how well the item differentiates among people at different locations.
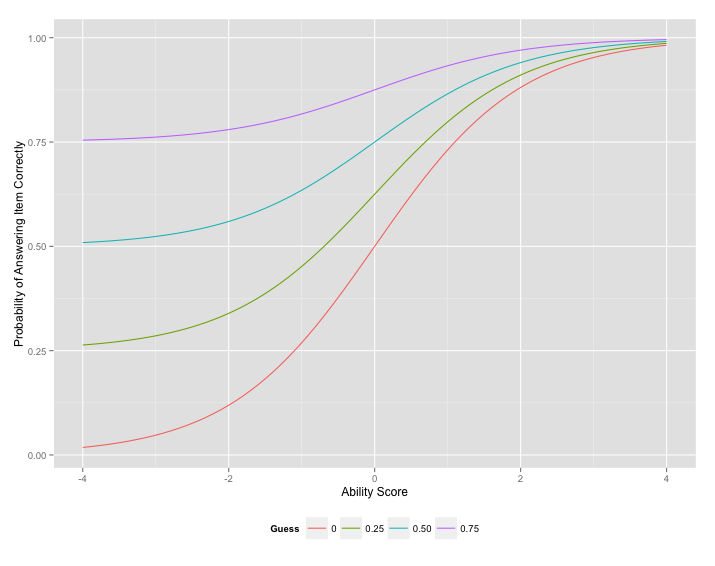
For the 3-PL, include item difficulty, item discrimination, and guessing
Guessing Parameter
Standard Error of Estimate and Information
Similar to the SEM, the standard error of estimate (SEE) allows us to quantify uncertainty about score of a person within IRT
Information is the inverse of the SEE and tells us how precise our estimates
We can use this to select items and develop tests!
See can also create 95% confidence intervals with this information
Item Information Function
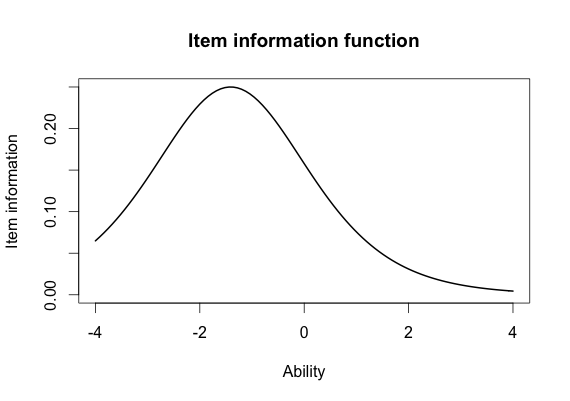
Test Information Function